代数、几何
1-两数之和
给定一个整数数组 nums 和一个目标值 target,在数组中找出和为 target 的两个整数,并返回他们的索引。
用哈希表存储 {key: nums[i], value: i},看要找的数是否在哈希表中。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> um;
for (int i = 0; i < nums.size(); ++i) {
int diff = target - nums[i];
if (um.find(diff) != um.end()) {
return {i, um[diff]};
}
um[nums[i]] = i;
}
return {};
}
};
15-三数之和
判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请��你找出所有满足条件且不重复的三元组。
N 个数的数组,穷举法需要枚举所有的组合数:N * (N-1) * (N-2),时间复杂度 O(n^3),要想优化它,可以先对数组进行排序。
排序后的数组,我们发现,当第一重循环 a 固定时,b 和 c 形成了一种“相互牵制”的关系,b 增大,c 就要减小,因此,b、c 可以分别从数组的两端向中间遍历,也就是“双指针”。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(), nums.end());
int n = nums.size() - 1;
for (int i = 0; i < n - 1; ++i) {
if (i > 0 && nums[i] == nums[i-1])
continue;
int lo = i + 1;
int hi = n;
while (lo < hi) {
int S = nums[i] + nums[lo] + nums[hi];
if (S == 0) {
res.push_back({nums[i], nums[lo], nums[hi]});
++lo;
--hi;
while (lo < hi && nums[lo] == nums[lo-1]) ++lo;
while (lo < hi && nums[hi] == nums[hi+1]) --hi;
} else if (S > 0) {
--hi;
} else {
++lo;
}
}
}
return res;
}
};
9-回文数
int 转 string:
class Solution {
public:
bool isPalindrome(int x) {
string s = to_string(x);
int lo = 0;
int hi = s.size() - 1;
while (lo < hi) {
if (s[lo++] != s[hi--]) return false;
}
return true;
}
};
数学解法,判断 1221 是否回文数:
1221 // 1000 = 1得到最高位1221 % 1000 = 1得到最低位1221 % 1000 // 10 = 22得到中间两位- 继续本过程
class Solution {
public:
bool isPalindrome(int x) {
// dividend 被除数
// divisor 除数
if (x < 0) return false;
int div = 1;
while (x / div >= 10)
div *= 10;
while (x > 0) {
if (x / div != x % 10)
return false;
x %= div;
x /= 10;
div /= 100;
}
return true;
}
};
11-盛最多水的容器

双指针限定容器的左右边界,因容器容量由高度较小的指针决定,因此每次移动高度较小的那一侧的指针。
class Solution {
public:
int maxArea(vector<int>& height) {
int lo = 0;
int hi = height.size() - 1;
int res = 0;
while (lo < hi) {
int w = hi - lo;
int h = min(height[lo], height[hi]);
res = max(res, w * h);
if (height[lo] < height[hi]) {
++lo;
}
else {
--hi;
}
}
return res;
}
};
42-接雨水
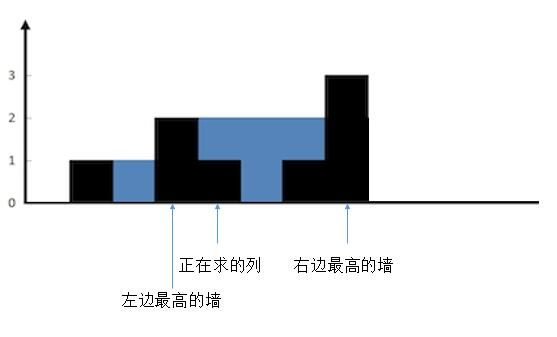
第一根与最后一根左右都是不接水的,因此忽略。
第 i 列能接多少雨水,取决于:
- i 左边的柱子最高的一根;i 右边的柱子最高的一根;两者的较小值。
- i 柱子比 (1) 找到的柱子矮,差值就是能接住的雨水。
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
vector<int> max_left(n);
vector<int> max_right(n);
int res = 0;
for (int i = 1; i < n - 1; ++i) {
max_left[i] = max(max_left[i-1], height[i-1]);
}
for (int i = n - 2; i >= 0; --i) {
max_right[i] = max(max_right[i+1], height[i+1]);
}
for (int i = 1; i < n - 1; ++i) {
int h = min(max_left[i], max_right[i]);
if (h > height[i]) {
res += h - height[i];
}
}
return res;
}
};
84-柱状图中最大的矩形
给定一组柱状图的高度,求能勾勒出的矩形的最大面积。
思路一,两重循环枚举矩形所有的底边(X 轴),对于每一个底边,矩形的高度是这些柱子的最低高度。时间复杂度 O(N^2)。
思路二,中心扩散法。一重循环枚举所有的柱子,对于每根柱子其高度为 h,向左右遍历找到高度为 h 的柱子所能划定的最大的矩形范围,就确定了矩形的左右边界。时间复杂度 O(N^2)。
思路二只用了一重循环,可以基于这个基础上进行优化,优化的思路是空间换时间。枚举每根柱子,其高度为 height[i],先考虑矩形的左边界,它由柱子左侧最近的高度小于 height[i] 的柱子决定;右边界同理。
以柱子 [6,7,5,2,4,5,9,3] 为例,我们可以用一个栈,保存“当前遍历的柱子,它左边会挡住它的那根柱子的高度”。
- 6 左边没有东西挡住,它的左边界是 -1(越界了,称为哨兵),此时栈为 [6]
- 7 左边被 6 挡住了,它的左边界是 6,此时栈为 [6, 7]
- 5 左边没有东西挡住,它的左边界是 -1,此时栈为 [5]
- 2 左边没有东西挡住,它的左边界是 -1,此时栈为 [2]
- 4 左边被 2 挡住了,它的左边界是 2,此时栈为 [2,4]
- 5 左边被 4 挡住了,它的左边界是 4,此时栈为 [2,4,5]
- 9 左边被 5 挡住了,它的左边界是 5,此时栈为 [2,4,5,9]
- 3 左边被 2 挡住了,它的左边界是 2,此时栈为 [2,3]
我们称这样一个栈为单调(递增)栈。由于高度可以直接从 height 数组中取,我们更需要的是下标的位置,因此我们不存高度而存的是下标。
单调栈的应用场景:在数组中对每一个数,找到第一个比自己小的元素。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
stack<int> mono_stk; // 单调栈
vector<int> left_bound(n, -1); // 记录 i 的左边界
vector<int> right_bound(n, n); // 记录 i 的右边界
for (int i = 0; i < n; ++i) {
while (!mono_stk.empty() && heights[mono_stk.top()] >= heights[i]) {
right_bound[mono_stk.top()] = i; // [1]
mono_stk.pop();
}
left_bound[i] = mono_stk.empty() ? -1 : mono_stk.top();
mono_stk.push(i);
}
int res = 0;
for (int i = 0; i < n; ++i) {
res = max(res, (right_bound[i] - left_bound[i] - 1) * heights[i]);
}
return res;
}
};
// [1] i 在栈顶柱子的右边,位于栈顶的柱子找右边界的时候会被 i 挡住,因此顺便把右边界也找出来了!
50-快速幂算法
计算 x 的 n 次幂。
本题的解法被称为「快速幂算法」,有递归和迭代两个版本。
递归版本,其思想是分治法,x ^ n = x ^ n/2 * x ^ n/2
class Solution {
public:
double myPow(double x, int n) {
if (n < 0) {
x = 1 / x;
n = abs(n);
}
if (n == 0) return 1;
if (n == 1) return x;
double y = myPow(x, n/2);
if (n % 2 == 0) {
return y * y;
} else {
return y * y * x;
}
}
};
迭代,其思想是二进制:

class Solution {
public:
double myPow(double x, int n) {
if (n < 0) {
x = 1 / x;
n = abs(n);
}
if (n == 0) return 1;
if (n == 1) return x;
double res = 1;
while (n > 0) {
if (n & 1 == 1) {
res *= x;
}
x *= x;
n >>= 1;
}
return res;
}
};
149-经过最多点的一条线
给定一个二维平面,平面上有 n 个点,求最多有多少个点在同一条直线上。
知识准备一:最大公约数。最大公约数的计算可以用素因数分解法、辗转相除法,后者效率更高。约定任何数
int gcd(int a, int b) {
if (b == 0) {
return a; // 约定 gcd(a, 0) = a
}
return gcd(b, a % b);
}
知识准备二:如何判断三点共线?直线方程——
- 一般式:
Ax + By + C = 0(A、B 不同时为 0),适用于所有直线。 - 点斜式:
y - y0 = k(x - x0),表示斜率为 k,且经过 (x0, y0) 的直线。适用于不垂直于 x 轴的直线。 - 截距式:
x / a + y / b = 1,表示与 x 轴、y 轴相交,且 x 轴截距为 a,y 轴截距为 b 的直线。适用于不过原点或不垂直于 x 轴、y 轴的直线。 - 斜截式:
y = kx + b,表示斜率为 k 且 y 轴截距为 b 的直线。适用于不垂直于 x 轴的直线。 - 两点式:
(y-y1)/(y2-y1)=(x-x1)/(x2-x1), (x1≠x2,y1≠y2),表示过 (x1, y1) 和 (x2, y2) 的直线。适用于不垂直于 x 轴、y 轴的直线。
struct Pair_hash {
template <typename T, typename U>
std::size_t operator()(const std::pair<T, U> &pair) const {
return std::hash<T>()(pair.first) ^ std::hash<U>()(pair.second);
}
};
// 求最大公约数
int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
class Solution {
public:
int maxPoints(const vector<vector<int>>& points) {
int N = static_cast<int>(points.size());
int res = 0;
for (int i = 0; i < N; ++i) {
vector<int> p0 = points[i];
int overlap = 0; // 记录重复的点
int pMax = 0;
unordered_map<pair<int, int>, int, Pair_hash> um; // 记录不同的直线斜率的出现次数
for (int j = i + 1; j < N; ++j) {
vector<int> p1 = points[j];
if (p0[0] == p1[0] && p0[1] == p1[1]) { // 重复的点
++overlap;
} else {
// p0, p1 组成一条直线
int deltaX = p1[0] - p0[0];
int deltaY = p1[1] - p0[1];
// 斜率存储前要约分
int g = gcd(deltaX, deltaY);
pair<int, int> pr(deltaX/g, deltaY/g);
++um[pr];
pMax = max(pMax, um[pr]);
}
}
pMax += overlap + 1;
res = max(res, pMax);
}
return res;
}
};
随机数
384-Shuffle an array
设计算法来打乱一个没有重复元素的数组。
问题等价于,给定一个数组,每次随机挑选出一个数,组成排列。这个排列要足够随机化,即所有排列的出现概率相同。
Fisher-Yates 洗牌算法。遍历数组,利用语言提供的随机函数,将当前遍历数与剩余所有数进行随机交换(注意,需包括自身在内)。每一步,都模拟了从剩余数组中随机挑选出一个数的过程。
C++ 中,要取得[a,b) 的随机整数,使用 rand() % (b-a) + a。
class Solution {
public:
Solution(vector<int>& nums) : origin(nums) {}
vector<int> reset() { return origin; }
vector<int> shuffle() {
vector<int> res(origin);
int N = origin.size();
for(int i = 0; i < N; ++i) {
swap(res[i], res[rand() % (N-i) + i]);
}
return res;
}
private:
const vector<int> origin;
};
398-随机选择一个索引
给定一个可能含有重复元素的整数数组,要求随机输出给定的数字的索引(给定的数字一定存在于数组中)。
方法一,通过一次遍历找到所有这个数字的索引,再使用随机函数取一个返回。时间复杂度 O(N),空间复杂度 O(N)。
方法二,蓄水池抽样法。
这种抽样方法的意义在于,我们并不知道即将到来的样本大小有多大,所以我们不适合将它们都写入内存再随机取。那么,我们把它当成一个数据流,每次一个数据到来,都按照 1/n 的概率来保留它,n 是目前的样本大小,最终就能得到均匀分布的随机样本。
class Solution {
public:
Solution(vector<int> &nums) : nums(nums) {}
int pick(int target) {
int found = 0;
int res = 0;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == target) {
++found;
int ran = rand() % found;
if (ran == found - 1) {
res = i; // 1/found 的概率保留
}
}
}
return res;
}
private:
vector<int> &nums;
};
470-用 Rand7() 实现 Rand10()
已有方法可生成 1 到 7 的均匀随机整数,写一个方法生成 1 到 10 的均匀随机整数。
数之间的运算无非就是加减乘除法。rand7 + rand7 的范围是 [2, 14],但分布不均匀;rand7 * rand7 的范围是 [1, 49],但分布也不均匀。
rand7 - 1 是 [0, 6] 之间随机,(rand7 - 1) * 7 是 [0, 7, 14, 21, 28, 35, 42] 之间随机。(rand7 - 1) * 7 + rand7 就得到 [1, 49] 之间的随机数。
存在这样一个规律,(randX - 1) * Y + randY = randXY,利用这个规律,我们可以得到 rand49。
对于 > 40 的数字我们直接丢弃(拒绝采样),剩余 [1, 40] 等概率出现。rand40 % 10 + 1 即可以得到 rand10。得到第一个 Accepted 的版本:
class Solution {
public:
int rand10() {
int ran = (rand7() - 1) * 7 + rand7();
if (ran <= 40) {
return ran % 10 + 1;
} else { // 拒绝采样,重新生成
return rand10();
}
}
};
它的期望时间复杂度是 O(1),但最坏情况下会达到 O(∞),即一直被拒绝。那么下一步优化的思路就是,如何利用这些被拒绝的采样。
上一轮拒绝采样的是 [1, 9] 内的随机数,利用上面的公式可以得到 rand7*9 = rand63。保留 [1, 60],拒绝 [1, 3],再次得到 rand21。此时保留 [1, 20],舍弃 21 即可。虽然理论上的最坏时间复杂度还是 O(∞),但实际上我们降低了调用 rand7 函数的期望次数。
class Solution {
public:
int rand10() {
int ran = (rand7() - 1) * 7 + rand7(); // rand49
if (ran <= 40)
return ran % 10 + 1;
ran -= 40;
ran = (rand7() - 1) * ran + rand7(); // rand63
if (ran <= 60)
return ran % 10 + 1;
ran -= 60;
ran = (rand7() - 1) * ran + rand7(); // rand21
if (ran <= 20)
return ran % 10 + 1;
return rand10();
}
};