设计题

有限状态机

有限状态自动机（FSM "Finite State Machine" 或者 FSA "Finite State Automaton"）解决一个输入序列，经过 FSM，最终停留在什么状态这样一个问题。构建 FSM 产出这样一个字典：在 x 状态下，输入 a，就会得到 y 状态。

8-字符串转换整数（atoi）

将字符串转换成整数。"42"、" -42"、"4193 with words"、"words and 987"、"-91283472332"……

每一位的字符，可能有 4 种情况：数字、+/-号、字母、空格。再加上考虑边界情况的处理，如果用 if...else... 结构，代码会写得比较臃肿。因此考虑用有限状态机。

class Automator {
public:
    Automator() {
        um["start"] = {"start", "sign", "number", "end"};
        um["sign"] = {"end", "end", "number", "end"};
        um["number"] = {"end", "end", "number", "end"};
        um["end"] = {"end", "end", "end", "end"};
    }

    int columnOf(char input) {
        if (isspace(input)) {
            return 0;
        } else if (input == '+' || input == '-') {
            return 1;
        } else if (isdigit(input)) {
            return 2;
        } else {
            return 3;
        }
    }

    void input(char c) {
        state = um[state][columnOf(c)];
        if (state == "number") {
            res = res * 10 + (c - '0');
            res = sign == 1 ? min(res, (long long)INT_MAX) : min(res, -(long long)INT_MIN);
        } else if (state == "sign") {
            sign = c == '+' ? 1 : -1;
        }
    }

    string state = "start"; // 当前状态
    int sign = 1; // 正负号
    long long res = 0; // 结果

private:
    unordered_map<string, vector<string>> um; // 数组 0,1,2,3 分别代表空格、符号、数字、字符
};

class Solution {
public:
    int myAtoi(string s) {
        Automator autom = Automator();
        for (char c : s) {
            autom.input(c);
            if (autom.state == "end") {
                break;
            }
        }
        int res = static_cast<int>(autom.sign * autom.res);
        return res;
    }
};

65-有效数字

393-UTF-8 编码验证

数据结构

146-LRU Cache

设计一个 LRU 缓存容器，支持以下接口：

LRUCache(int capacity) 初始化时传入容器的容量。

int get(int key) 如果 key 存在于容器中则返回 value，否则返回 -1。

void put(int key, int value) 如果 key 存在则更新其 value；否则插入键值对。当超出容量时，移除最久未使用的值。

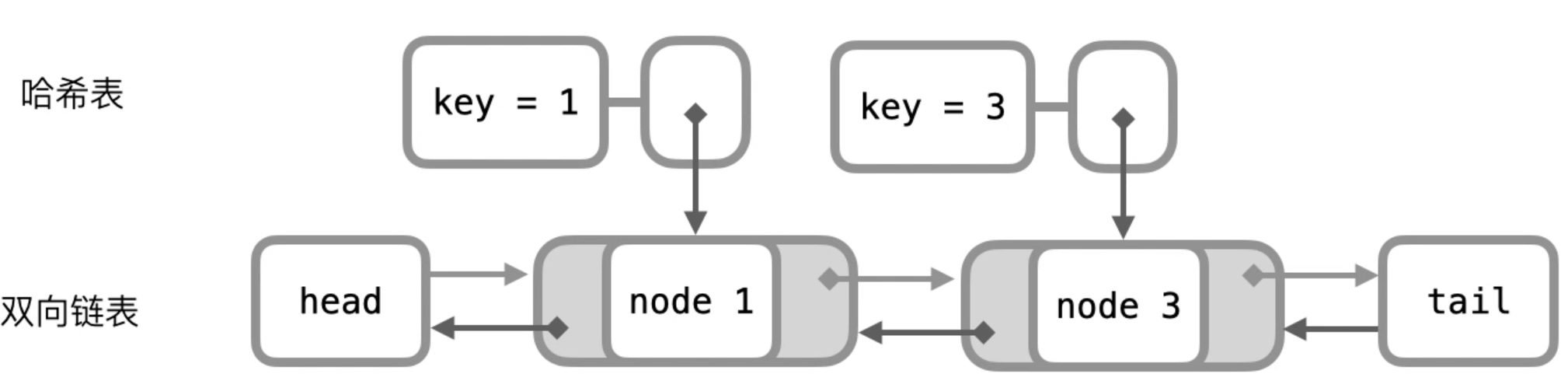
实现本题的两种操作，需要用到一个哈希表和一个双向链表。

哈希表存储键到双向链表中的节点的映射。

链表要存储头节点；双向链表要存储头、尾两个节点。靠近头部的键值对是最近使用的，靠近尾部的键值对是最久未使用的。

#include <unordered_map>
using std::unordered_map;

#include <memory>
using std::shared_ptr;
using std::make_shared;

struct Node {
    Node(int k, int v) : key(k), val(v) {}
    int key;
    int val;
    shared_ptr<Node> pre = nullptr;
    shared_ptr<Node> next = nullptr;
};

class LRUCache {
public:
    LRUCache(int capacity) : capacity(capacity) {
        // 伪头部和尾部节点，不实际存储键值对
        head->next = tail;
        tail->pre = head;
    }
    int get(int key) {
        if (um.find(key) != um.end()) {
            shared_ptr<Node> node = um[key];
            moveToHead(node);
            return node->val;
        } else {
            return -1;
        }
    }
    void put(int key, int value) {
        if (um.find(key) != um.end()) {
            shared_ptr<Node> node = um[key];
            node->val = value;
            moveToHead(node);
        } else {
            shared_ptr<Node> node = make_shared<Node>(key, value);
            um[key] = node;
            addToHead(node);
            ++size;
            if (size > capacity) {
                shared_ptr<Node> tail = removeTail();
                um.erase(tail->key);
                --size;
            }
        }
    }
private:
    int capacity; // 容量
    int size = 0; // 容器当前大小
    unordered_map<int, shared_ptr<Node>> um; // key -> 节点
    shared_ptr<Node> head = make_shared<Node>(0, 0); // 头部是最近使用的
    shared_ptr<Node> tail = make_shared<Node>(0, 0); // 尾部是最久未使用的

    void moveToHead(shared_ptr<Node> node) {
        removeNode(node);
        addToHead(node);
    }
    void addToHead(shared_ptr<Node> node) {
        node->pre = head;
        node->next = head->next;
        head->next->pre = node;
        head->next = node;
    }
    void removeNode(shared_ptr<Node> node) {
        node->next->pre = node->pre;
        node->pre->next = node->next;
    }
    shared_ptr<Node> removeTail() {
        shared_ptr<Node> tmp = tail->pre; // 注意，这才是真正的尾巴！
        removeNode(tmp);
        return tmp;
    }
};

155-最小栈

设计一个支持 push, pop, top 操作，并能在常数时间内检索到最小元素的栈。

解决这个问题要用到一个辅助栈，每次 push 操作，将数压入普通栈、同时将当前最小值压入辅助栈，使他们同进同出、一一对应。

class MinStack {
public:
    void push(int x) {
        x_stack.push(x);
        if (min_stack.empty()) {
            min_stack.push(x);
        } else {
            min_stack.push(min(min_stack.top(), x));
        }
    }
    void pop() {
        x_stack.pop();
        min_stack.pop();
    }
    int top() {
        return x_stack.top();
    }
    int getMin() {
        return min_stack.top();
    }
private:
    stack<int> x_stack;
    stack<int> min_stack;
};

225-用队列实现栈

插入后，将队列的前 N 个元素依次出队并入队。插入操作是 O(N)，其余是 O(1)。

class MyStack {
public:
    void push(int x) {
        int size = q.size();
        q.push(x);
        for (int i = 0; i < size; ++i) {
            q.push(q.front());
            q.pop();
        }
    }
    int pop() {
        int front = q.front();
        q.pop();
        return front;
    }
    int top() {
        return q.front();
    }
    bool empty() {
        return q.empty();
    }
private:
    queue<int> q;
};

232-用栈实现队列

class MyQueue {
public:
    void push(int x) {
        int size = stk1.size();
        for (int i = 0; i < size; ++i) {
            stk2.push(stk1.top());
            stk1.pop();
        }
        stk1.push(x);
        for (int i = 0; i < size; ++i) {
            stk1.push(stk2.top());
            stk2.pop();
        }
    }
    int pop() {
        int top = stk1.top();
        stk1.pop();
        return top;
    }
    int peek() {
        return stk1.top();
    }
    bool empty() {
        return stk1.empty();
    }
private:
    stack<int> stk1;
    stack<int> stk2;
};

895-最大频率栈

这题使用到的数据结构比较巧妙，除了常规的数字到出现频次的字典；还需要一个频次到栈的字典。

class FreqStack {
public:
    void push(int val) {
        freq[val] += 1;
        int f = freq[val];
        maxFreq = max(f, maxFreq);
        group[f].push(val);
    }

    int pop() {
        int res = group[maxFreq].top();
        group[maxFreq].pop();
        if (group[maxFreq].empty()) {
            maxFreq -= 1;
        }
        freq[res] -= 1;
        return res;
    }
private:
    unordered_map<int, int> freq; // 数 -> 频次
    unordered_map<int, stack<int>> group; // 频次 -> 该频次下的数
    int maxFreq; // 当前最大频次
};

分析代码执行过程可以得知，频次是从 1 开始的连续数字，因此，group 这个字典也可以用数组代替。