字符串

回文

回文是正着读、反着读都一样的字符串。

125-验证回文串（双指针或双向队列）

双指针：

class Solution {
public:
    bool isPalindrome(string s) {
        int n = s.size();
        int i = 0;
        int j = n - 1;
        while (i < j) {
            while (i < j && !isalnum(s[i])) ++i;
            while (i < j && !isalnum(s[j])) --j;
            if (tolower(s[i]) != tolower(s[j])) return false;
            ++i;
            --j;
        }
        return true;
    }
};

双向队列：

class Solution {
public:
    bool isPalindrome(string s) {
        int N = s.size();
        deque<char> dq;
        for (const char &c : s) {
            if (isalnum(c)) {
                dq.push_back(tolower(c));
            }
        }
        while (dq.size() >= 2) {
            if (dq.front() != dq.back())
                return false;
            dq.pop_front();
            dq.pop_back();
        }
        return true;
    }
};

5-最长回文子串（中心扩散法）

给定一个字符串，找到其中最长的回文子串。

对于回文子串问题，中心扩散法是更优的解法。长度为 N 的字符串 s[0...n-1] 一共有 2N-1 个中心扩散点。

class Solution {
public:
    void expand(const string &s, int i, int j) {
        if (i > j) return;
        while (i >= 0 && j < s.size() && s[i] == s[j]) {
            --i;
            ++j;
        }
        ++i;
        --j;
        if (hi - lo < j - i) {
            lo = i;
            hi = j;
        }
    }
    string longestPalindrome(const string &s) {
        for (int i = 0; i < s.size(); ++i) {
            expand(s, i, i);
            expand(s, i, i + 1);
        }
        return s.substr(lo, hi - lo + 1);
    }
private:
    int lo = 0;
    int hi = 0;
};

647-回文子串（中心扩散法）

给定一个字符串，计算这个字符串中有多少个回文子串。

对于回文子串问题，中心扩散法是更优的解法。

class Solution {
public:
    void expand(const string &s, int i, int j) {
        if (i > j) return;
        while (i >= 0 && j < s.size() && s[i] == s[j]) {
            ++res;
            --i;
            ++j;
        }
    }
    int countSubstrings(const string &s) {
        for (int i = 0; i < s.size(); ++i) {
            expand(s, i, i);
            expand(s, i, i + 1);
        }
        return res;
    }
private:
    int res = 0;
};

516-最长回文子序列（动态规划）

回文问题要抓住一个基本特征，就是中间向两边扩散。假设有字符串 s，我们如果已知 s[i...j] 的最长回文子序列的长度，那么当 i、j 分别向左右扩散时，我们就可以利用 dp[i][j] 的结果进行扩展，因此本题可以用动态规划求解。

假设字符串为 "abcbd"，长度为 5，我们画一个 5x5 的表格，dp[i][j] 表示 s[i...j] 中的最长回文子序列的长度。很显然，这个表格只有当列数 > 行数时才有意义。

一、最优子结构：dp[i][j] 表示 s[i...j] 中的最长回文子序列的长度。

二、状态转移方程

• 如果 i == j，dp[i][j] = 1
• 如果 s[i] == s[j]，则 dp[i][j] = dp[i+1][j-1] + 2

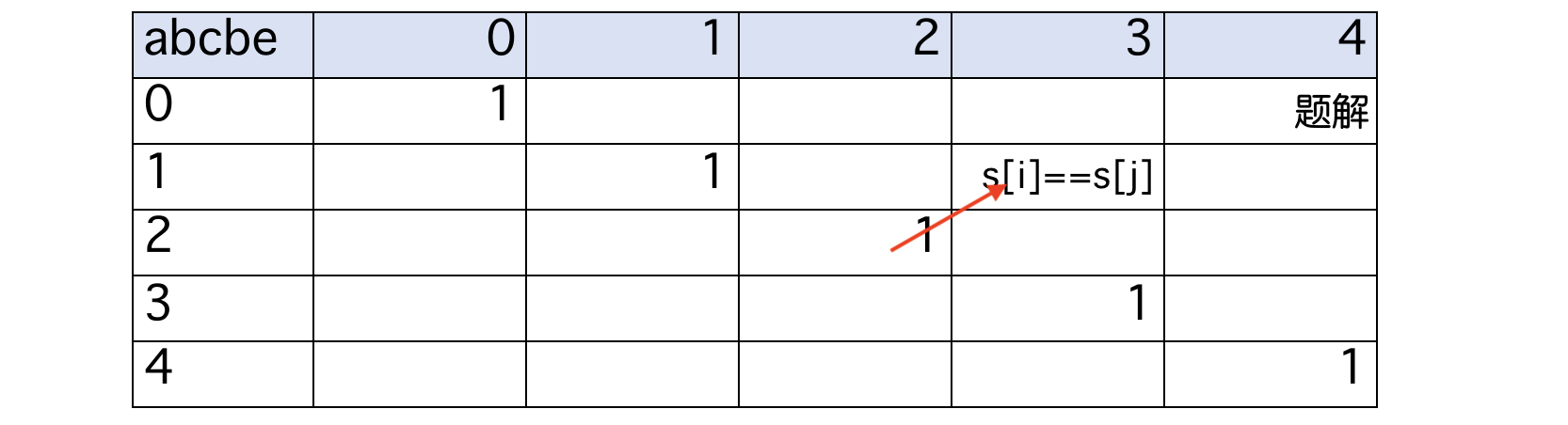
• 如果 s[i] != s[j]，dp[i][j] = max(dp[i+1][j], dp[i][j-1])

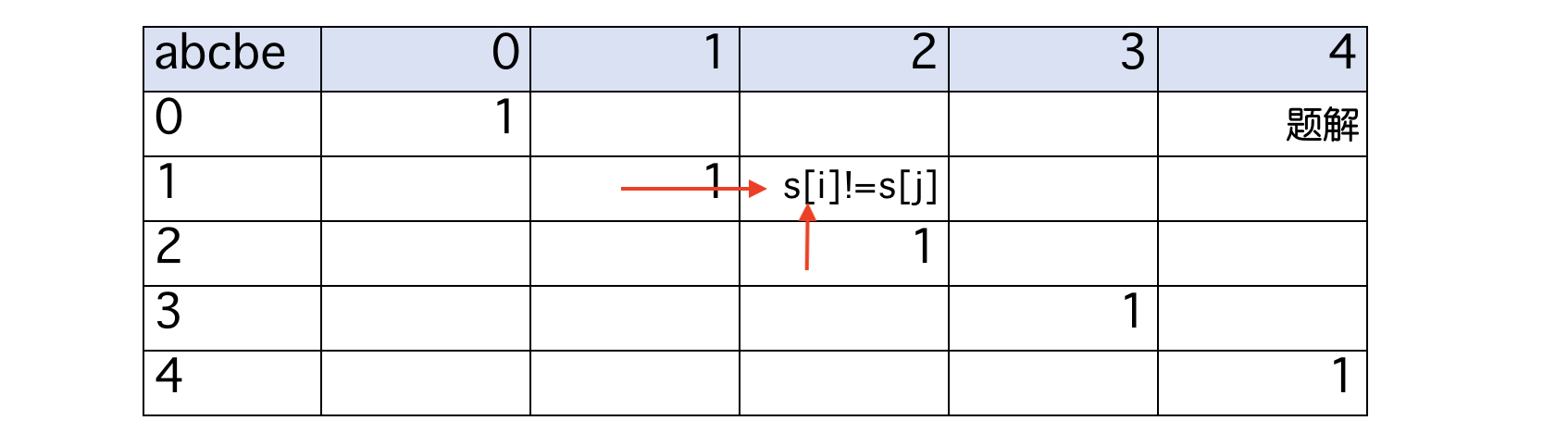
dp[0][n-1] 表示 s[0..<n] 中的最长回文子序列长度，因此题解在表格的右上方，遍历方向是从下至上、从左至右。

class Solution {
public:
    int longestPalindromeSubseq(const string &s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j) {
                if (i == j) {
                    dp[i][j] = 1;
                } else if (s[i] == s[j]) {
                    dp[i][j] = dp[i+1][j-1] + 2;
                } else {
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][n-1];
    }
};

子串问题（滑动窗口 + 哈希表）

3-无重复字符的最长子串

给定一个字符串，找出其中不含有重复字符的最长子串的长度。

子串问题的特征是，给定一个字符串，找到符合某种条件的子串。通用的解决办法是滑动窗口 + 哈希表。

需要一个哈希表记录每个字符出现的位置。

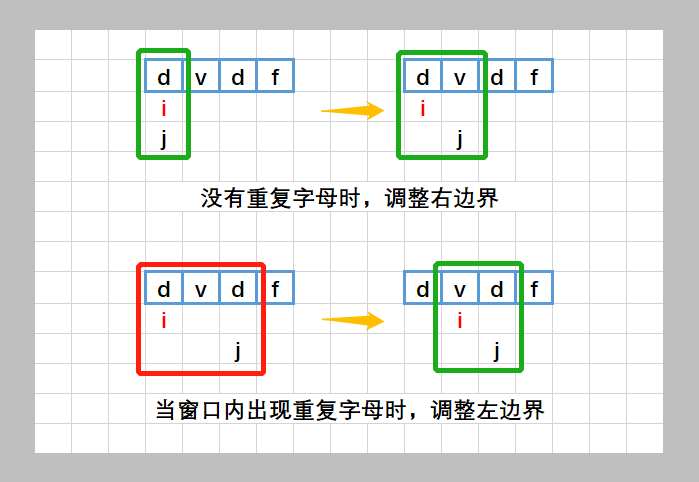
i 只能右移，不能左移，当发现了重复字符，i = max(i, 重复字符的位置 + 1)，为什么？因为左移的话，刚才已经排除掉的其它重复字符又会包括进来。

class Solution {
public:
    int lengthOfLongestSubstring(const string &s) {
        int i = 0;
        int j = 0;
        int res = 0;
        unordered_map<char, int> um;
        while (j < s.size()) {
            if (um.find(s[j]) != um.end()) {
                i = max(i, um[s[j]] + 1); // 使 i...j 不包括重复字符
            }
            um[s[j]] = j;
            res = max(res, j - i + 1);
            ++j;
        }
        return res;
    }
};

76-包含了指定字符的最小子串

给定一个字符串，找出其中包含了指定字符的最小子串。注意：如果 s 中存在这样的子串，我们保证它是唯一答案。

步骤一：不断增加 j 使滑动窗口增大，直到窗口包含了 t 中所有字符。

步骤二：不断增加 i 使滑动窗口缩小，将不必要的元素排除在外，直到碰到一个必须包含的元素，这个时候不能再扔了，再扔就不满足条件了，保存此时滑动窗口的位置。

步骤三：让 j 继续增加，直到碰到 s[j] == s[i]，此时 s[i] 找到了“接班人”，可以被排除在外了，i 继续增加。

需要一个哈希表记录指定的每个字符及其出现次数。计数为正的表示仍然需要的元素数量，计数为负的表示多余的元素数量、计数为 0 表示刚刚好。

例如 need 等于 {'A':-2,'B':0,'C':1} 时，A 多余 2 个，B 正好，C 还缺 1 个。

python3：Counter 是 dict 的子类，用于计数可哈希对象。Counter 对象有一个字典接口，如果引用的键没有任何记录，就返回一个 0，而不是弹出一个 KeyError。

class Solution {
public:
    string minWindow(const string &s, const string &t) {
        unordered_map<char, int> um;
        for (const char &c : t) {
            ++um[c];
        }
        int found = 0;
        int N = s.size();
        int lo = 0;
        int hi = N;
        int i = 0;
        int j = 0;
        while (j < N) {
            if (um[s[j]] > 0) {
                ++found;
            }
            --um[s[j]];
            if (found == t.size() && (hi == N || s[j] == s[i])) {
                // 找到 t 中的所有字符了，但此时可能有很多其它字符包括了进来
                // 多余的字符，在字典中的计数为负数
                while (i < j) {
                    if (um[s[i]] == 0) break;
                    ++um[s[i]];
                    ++i;
                }
                if (j - i < hi - lo) {
                    lo = i;
                    hi = j;
                }
                // 第一次找齐：found == t.size() && hi == N
                // 第二次或以后找齐：found == t.size() && s[i] == s[j]，必须找到一个与左指针指向字符相同的字符，左指针才能右移
            }
            ++j;
        }
        if (found < t.size()) return "";
        return s.substr(lo, hi - lo + 1);
    }
};

字符串处理

14-最长公共前缀

给定一组字符串，求它们的最长公共前缀。

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (strs.empty() || strs[0].empty()) return "";
        string res = "";
        for (int i = 0; i < strs[0].size(); ++i) {
            for (int j = 1; j < strs.size(); ++j) {
                if (strs[j][i] != strs[0][i]) {
                    return res;
                }
            }
            res += strs[0][i];
        }
        return res;
    }
};

20-括号匹配

借助栈数据结构。

class Solution {
public:
    bool match(const char &lhs, const char &rhs) {
        return lhs == '(' && rhs == ')' || lhs == '{' && rhs == '}' || lhs == '[' && rhs == ']';
    }
    bool isValid(const string &s) {
        stack<char> stk;
        for (const char &c : s) {
            if (c == ')' || c == ']' || c == '}') {
                if (stk.empty()) return false;
                if (!match(stk.top(), c)) return false;
                stk.pop();
            } else {
                stk.push(c);
            }
        }
        return stk.empty();
    }
};

242-字母异位词

方法一：哈希表计数；方法二：字符串排序后比较。

class Solution {
public:
    bool isAnagram(const string &s, const string &t) {
        if (s.size() != t.size()) return false;
        unordered_map<char, int> um1;
        unordered_map<char, int> um2;
        for (const char &c : s) {
            ++um1[c];
        }
        for (const char &c : t) {
            ++um2[c];
        }
        return um1 == um2;
    }
};

151-按单词翻转字符串

按单词翻转字符串。

输入：" Bob Loves Alice "；

输出 "Alice Loves Bob"。

字符串流可以解决句首、句尾、单词中间多余的空格问题。

class Solution {
public:
    string reverseWords(string s) {
        vector<string> vec;
        string res;
        stringstream ss(s);
        string str;
        while (ss >> str) {
            vec.push_back(str);
        }
        for (int i = vec.size() - 1; i >= 0; --i) {
            res += vec[i];
            res += " "; // 最后多了一个空格，返回答案时要截掉
        }
        if (!res.empty()) {
            res = string(res.begin(), res.end() - 1);
            // 等价于
            // res = res.substr(0, res.size() - 1);
        }
        return res;
    }
};

原地翻转方案。先整体翻转，再逐个单词翻转，最后，同向双指针覆写去除多余空格。

class Solution {
public:
    string reverseWords(string s) {
        reverse(s.begin(), s.end());
        int lo = 0;
        int hi = s.size() - 1;
        while (lo < hi && isspace(s[lo]))
            ++lo; // 去掉句首空格
        while (lo < hi && isspace(s[hi]))
            --hi; // 去掉句尾空格
        int i = lo;
        while (i <= hi) {
            while (isspace(s[i]) && i < hi)
                ++i; // 单词的左边界
            int j = i;
            while (!isspace(s[j]) && j <= hi)
                ++j; // 单词的右边界
            reverse(s.begin() + i, s.begin() + j);
            i = j;
        }
        // 去掉句中冗余空格：快慢指针覆写
        int slow = lo + 1;
        for (int quick = slow; quick <= hi; ++quick) {
            if (isspace(s[quick]) && isspace(s[quick-1])) {
                continue;
            }
            s[slow] = s[quick];
            ++slow;
        }
        return s.substr(lo, slow - lo);
    }
};

557-反转字符串中的每个单词 III

输入："Let's take LeetCode contest"。

输出："s'teL ekat edoCteeL tsetnoc"。

stringstream 方案：

class Solution {
public:
    string reverseWords(string s) {
        stringstream ss(s);
        string str;
        vector<string> vec;
        while (ss >> str) {
            reverse(str.begin(), str.end());
            vec.push_back(str);
        }
        string res;
        for (string s : vec) {
            res += s;
            res += " ";
        }
        return res.substr(0, res.size() - 1);
    }
};

原地反转方案：

class Solution {
public:
    string reverseWords(string s) {
        int lo = 0;
        int hi = s.size() - 1;
        while (lo <= hi) {
            while (isspace(s[lo]) && lo < hi)
                ++lo;
            int j = lo;
            while (!isspace(s[j]) && j <= hi)
                ++j;
            reverse(s.begin() + lo, s.begin() + j);
            lo = j;
        }
        return s;
    }
};