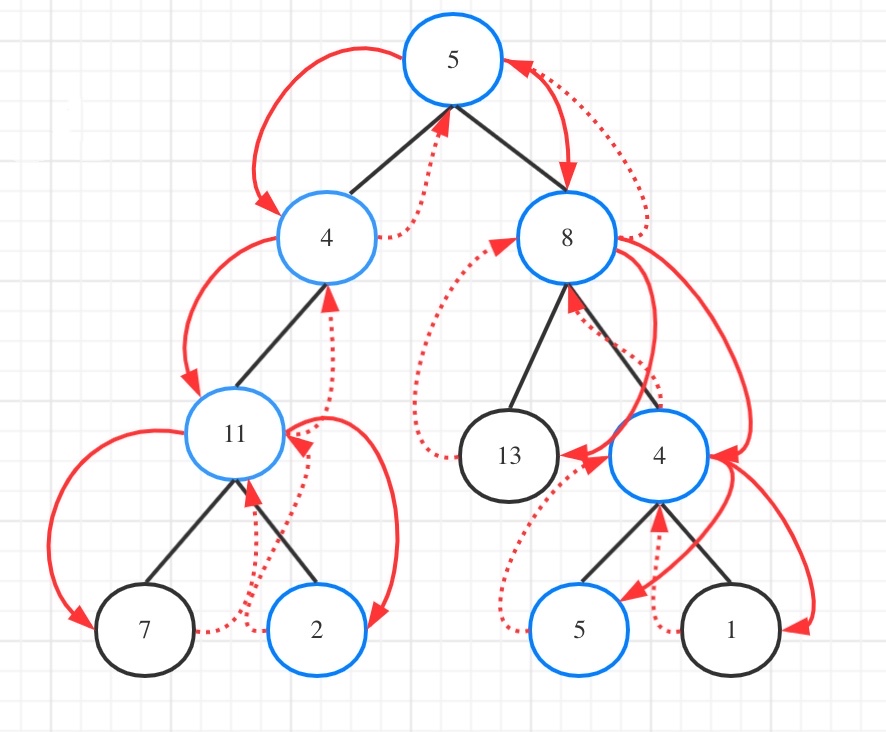
树
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
TreeNode() : TreeNode(0, nullptr, nullptr) {}
TreeNode(int x) : TreeNode(x, nullptr, nullptr) {}
};
树的遍历
94-二叉树中序遍历、144-二叉树前序遍历、145-二叉树后序遍历
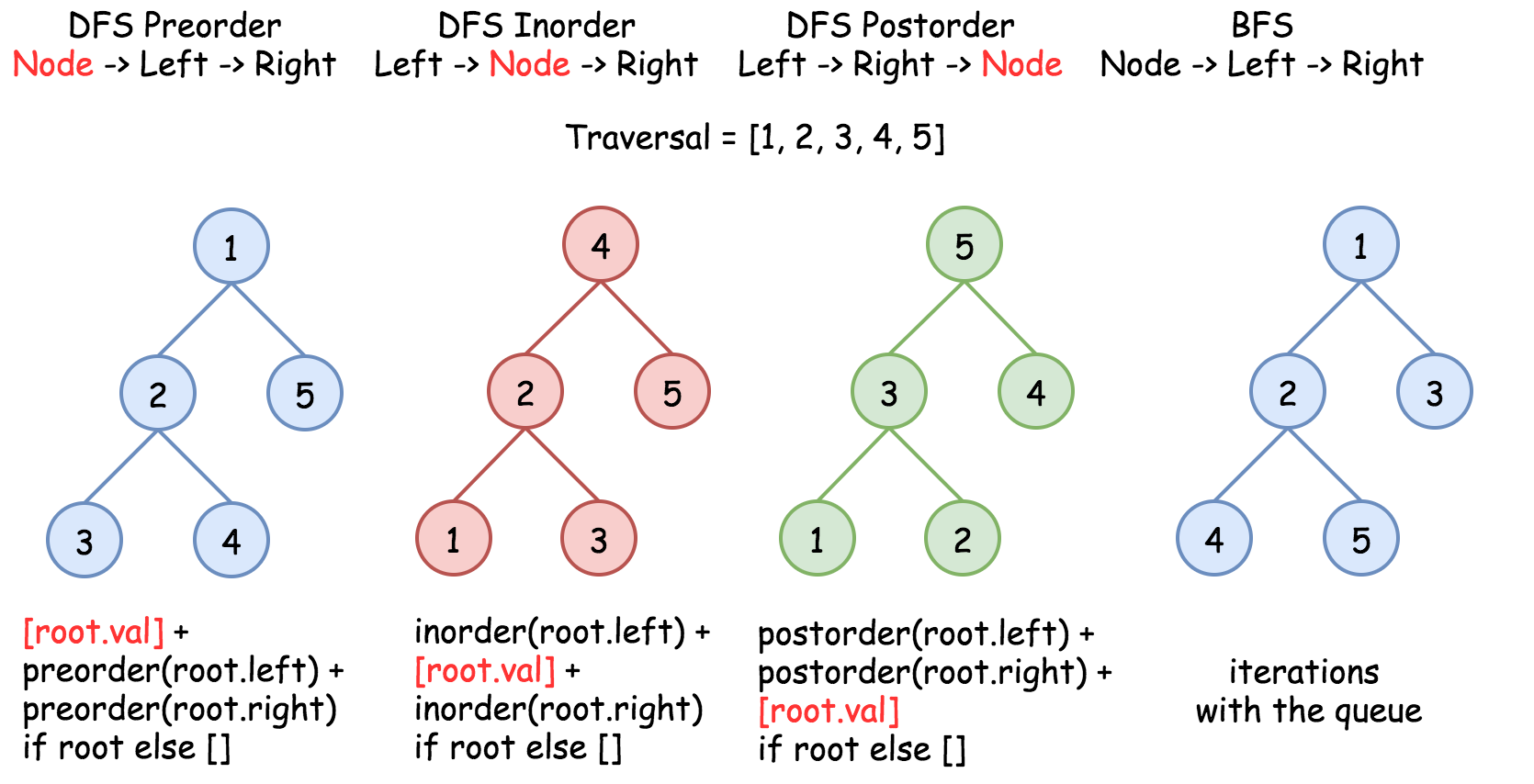
几乎所有的二叉树问题,都可以用 DFS 来解决。
class Solution {
public:
void dfs(TreeNode *root, vector<int> &res) {
if (!root) return;
// preorder
dfs(root->left, res);
res.push_back(root->val); // inorder
dfs(root->right, res);
// postorder
}
vector<int> inorderTraversal(TreeNode *root) {
vector<int> res;
dfs(root, res);
return res;
}
};
递归实现时,是函数调用自身,一层层地嵌套下去,操作系统自动帮我们用栈来保存了每个调用的函数;如果不用递归实现,我们可以用栈来模拟这个调用过程。(这种方法比较不直观,且前序、中序、后序不一样,很难记忆)
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while (root || stk.size() != 0) {
while (root) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
res.push_back(root->val);
root = root->right;
}
return res;
}
};
102-二叉树层序遍历
在实际使用中,我们用 DFS 的时候远远多于 BFS。不过,某些场景是 DFS 做不到的,只能使用 BFS,比如“层序遍历”。
BFS 会用到队列数据结构:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode *root) {
vector<vector<int>> res;
if (!root) return res;
queue<TreeNode *> q;
q.push(root);
while (!q.empty()) {
vector<int> level;
int size = static_cast<int>(q.size());
for (int i = 0; i < size; ++i) {
TreeNode *front = q.front();
q.pop();
level.push_back(front->val);
if (front->left) {
q.push(front->left);
}
if (front->right) {
q.push(front->right);
}
}
res.push_back(level);
}
return res;
}
};
429-N 叉树的层序遍历
扩展到 N 叉树的层序遍历:
class Solution {
public:
vector<vector<int>> levelOrder(Node *root) {
vector<vector<int>> res;
if (!root) return res;
queue<Node *> queue;
queue.push(root);
while (!queue.empty()) {
vector<int> level;
int size = queue.size();
for (int i = 0; i < size; ++i) {
root = queue.front();
queue.pop();
level.push_back(root->val);
for (Node *node : root->children) {
queue.push(node);
}
}
res.push_back(level);
}
return res;
}
};
199-二叉树的右视图
第一种思路,dfs 前序遍历,我们按照根结点 -> 右子树 -> 左子树的顺序访问,就可以保证每层都最先访�问最右边的节点。
关键是,如何判断每层访问的第一个节点呢?可以用遍历深度来限定。由于每层只取最右边节点的值加入 res 数组,若数组长度与遍历深度相同,说明是该层访问的第一个节点,把它加到 res 数组中。
class Solution {
public:
void dfs(TreeNode *root, vector<int> &res, int level) {
if (!root) return;
if (res.size() == level)
res.push_back(root->val);
dfs(root->right, res, level + 1);
dfs(root->left, res, level + 1);
}
vector<int> rightSideView(TreeNode *root) {
vector<int> res;
dfs(root, res, 0);
return res;
}
};
第二种思路,bfs 层序遍历:
class Solution {
public:
vector<int> rightSideView(TreeNode *root) {
vector<int> res;
if (!root) return res;
queue<TreeNode *> queue;
queue.push(root);
int level = 0;
while (!queue.empty()) {
int size = queue.size();
for (int i = 0; i < size; ++i) {
root = queue.front();
queue.pop();
if (res.size() == level)
res.push_back(root->val);
if (root->right)
queue.push(root->right); // 先放右边的节点
if (root->left)
queue.push(root->left);
}
++level;
}
return res;
}
};
124-二叉树中的最大路径和
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。
找到递归结构是本题的关键!定义函数 dfs(root),它的返回值是以 root 为起点的树的最大路径和。
那么,以 root 为起点的树的最大路径和 = root->val + max(root->left 或 0,root->right 或 0),这是一个后序遍历!
注意,计算最大和这种问题,都需要考虑负数的情况,如果树的左/右支的最大和为负数,那么我们会“剪枝”。
本题中路径可以是任意节点出发到任意节点,不一定要以根结点为起点。因此,在执行每一次递归时,需要将 root 作为“连接点”,计算(根节点 + 左子树最大路径和 + 右子树最大路径和)是否成为全局最优解。
class Solution {
public:
int dfs(TreeNode *root, int &res) {
if (!root) return 0;
int left = max(0, dfs(root->left, res)); // 左子树的最大路径和,或 0(剪枝)
int right = max(0, dfs(root->right, res)); // 右子树的最大路径和,或 0(剪枝)
res = max(res, left + right + root->val);
return max(left, right) + root->val;
}
int maxPathSum(TreeNode *root) {
int res = root->val;
dfs(root, res);
return res;
}
};
105-从前序与中序遍历序列构造二叉树
树中没有重复元素。
只有中序+前序、中序+后序可以唯一确定一棵二叉树。
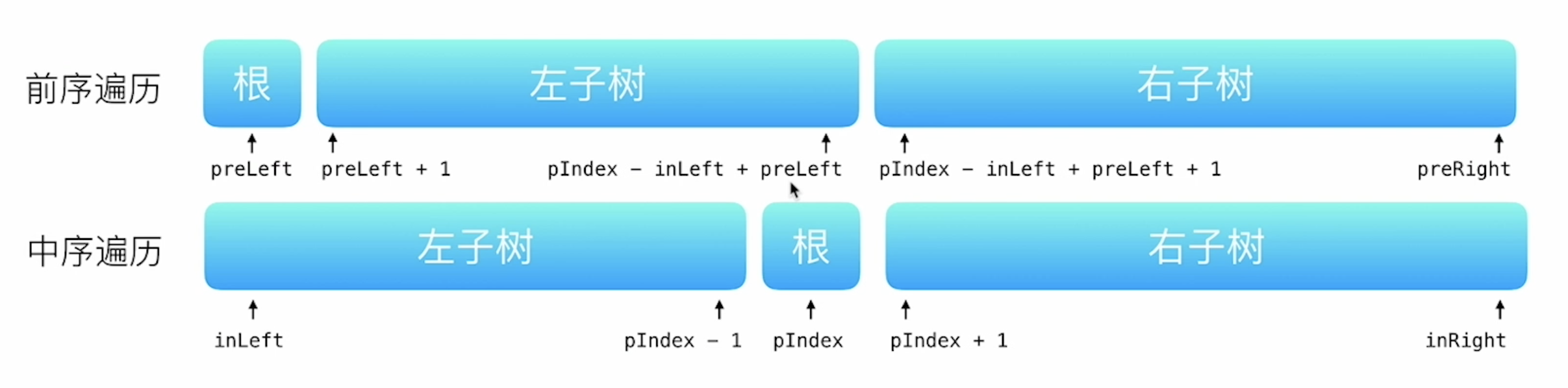
根据前序遍历得到根节点,然后在中序遍历中找到根节点的位置,它的左边就是左子树的节点,右边就是右子树的节点。这很明显是一个前序遍历的过程。
class Solution {
public:
TreeNode* build(vector<int>& preorder, int preLeft, int preRight, vector<int>& inorder, int inLeft, int inRight, unordered_map<int, int> &um) {
if (preLeft > preRight || inLeft > inRight) return nullptr;
TreeNode *root = new TreeNode(preorder[preLeft]);
int pIndex = um[root->val];
root->left = build(preorder, preLeft + 1, preLeft + pIndex - inLeft, inorder, inLeft, pIndex - 1, um);
root->right = build(preorder, preLeft + pIndex - inLeft + 1, preRight, inorder, pIndex + 1, inRight, um);
return root;
}
TreeNode *buildTree(vector<int>& preorder, vector<int>& inorder) {
unordered_map<int, int> um;
for (int i = 0; i < inorder.size(); ++i) {
um[inorder[i]] = i; // value -> position
}
return build(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1, um);
}
};
106-从中序与后序遍历序列构造二叉树
根 - 左 - 右,前序遍历。
class Solution {
public:
TreeNode *build(vector<int>& inorder, int inLeft, int inRight, vector<int>& postorder, int postLeft, int postRight, unordered_map<int, int> &um) {
if (inLeft > inRight || postLeft > postRight) return nullptr;
TreeNode *root = new TreeNode(postorder[postRight]);
int pIndex = um[root->val];
root->left = build(inorder, inLeft, pIndex - 1, postorder, postLeft, postLeft + pIndex - inLeft - 1, um);
root->right = build(inorder, pIndex + 1, inRight, postorder, postLeft + pIndex - inLeft, postRight - 1, um);
return root;
}
TreeNode *buildTree(vector<int>& inorder, vector<int>& postorder) {
unordered_map<int, int> um;
for (int i = 0; i < inorder.size(); ++i) {
um[inorder[i]] = i;
}
return build(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1, um);
}
};
100-相同的树
根节点相同、左子树相同、右子树也相同,这是一个前序遍历。
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (!p && !q) return true;
if (p && q) {
if (p->val != q->val) return false;
if (!isSameTree(p->left, q->left)) return false;
if (!isSameTree(p->right, q->right)) return false;
return true;
}
return false;
}
};
101-对称二叉树
若 p 和 q 相同,p.left 和 q.right 相同,p.right 和 q.left 相同,则为对称,这是一个前序遍历。
class Solution {
public:
bool dfs(TreeNode *p, TreeNode *q) {
if (!p && !q) return true;
if (p && q) {
if (p->val != q->val) return false;
if (!dfs(p->left, q->right)) return false;
if (!dfs(p->right, q->left)) return false;
return true;
}
return false;
}
bool isSymmetric(TreeNode* root) {
if (!root) return true;
return dfs(root->left, root->right);
}
};
104-二叉树的最大深度
二叉树的最大深度等于 max(左子树的深度,右子树的深度) + 1,这是一个后序遍历。
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) return 0;
int left = maxDepth(root->left);
int right = maxDepth(root->right);
return max(left, right) + 1;
}
};
129-根到叶子节点数字之和
从根到叶子节点路径 1->2->3 代表数字 123。计算从根到叶子节点生成的所有数字之和。
每深入一层,数字和等于(上一层的结果乘以 10 + 当前节点值)。若当前到达叶子结点,则得到一个和;否则,分别向左、右子树深入,这是一个前序遍历,
class Solution {
public:
int dfs(TreeNode *root, int path) {
if (!root) return 0;
path = path * 10 + root->val;
if (!root->left && !root->right)
return path;
return dfs(root->left, path) + dfs(root->right, path);
}
int sumNumbers(TreeNode* root) {
return dfs(root, 0);
}
};
226-翻转二叉树
后序遍历
class Solution {
public:
TreeNode* invertTree(TreeNode *root) {
if (!root) return nullptr;
TreeNode *left = invertTree(root->right);
TreeNode *right = invertTree(root->left);
root->left = left;
root->right = right;
return root;
}
};
236-二叉树的最近公共祖先
The lowest common ancestor (LCS) is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).
后序遍历,找到 p 或 q 就返回。
- 若 root == p 或 q,那么 root 就是 p、q 的最近公共祖先(p 或 q 本身);
- 向左、右子树分别查找 p 或 q;若都不为空,说明 p、q 分别在左右子树中,那么 LCS 就是 root。
- 如果仅左子树不为空,p 和 q 存在左子树内,返回左子树;右子树同理。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root || root == p || root == q) return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if (!left) return right;
if (!right) return left;
return root;
}
};
二叉搜索树
BST 的中序遍历是一个有序数组,BST 有关的问题都是利用这个特性解决。
99-恢复二叉搜索树
一棵 BST 中的两个节点被错误地交换。在不改变其结构的情况下,恢复这棵树。
思路是,中序遍历,观察问题的特点:被交换的节点不相邻 [5, 2, 3, 4, 1] 或相邻 [2, 1, 3, 4, 5]。
记住前一个节点并与当前节点比较,发现并记住乱序的两个节点,最后交换值即可。
class Solution {
public:
void dfs(TreeNode *root) {
if (!root) return;
dfs(root->left);
if (pre && root->val < pre->val) {
if (!first) {
first = pre;
}
second = root;
}
pre = root;
dfs(root->right);
}
void recoverTree(TreeNode* root) {
dfs(root);
swap(first->val, second->val);
}
private:
TreeNode *first;
TreeNode *second;
TreeNode *pre;
};
98-验证二叉搜索树
给定一棵二叉树,验证其是否 BST。
中序遍历,记住前一个节点并与当前节点比较。
class Solution {
public:
bool isValidBST(TreeNode *root) {
if (!root) return true;
if (!isValidBST(root->left))
return false;
if (cur && cur->val >= root->val)
return false;
cur = root;
if (!isValidBST(root->right))
return false;
return true;
}
private:
TreeNode *cur;
};
108-将有序数组转换为二叉搜索树
有序数组转换成 BST 有多种答案。
class Solution {
public:
TreeNode *build(vector<int>& nums, int lo, int hi) {
if (lo > hi) return nullptr;
int mid = lo + (hi - lo) / 2;
TreeNode *root = new TreeNode(nums[mid]);
root->left = build(nums, lo, mid - 1);
root->right = build(nums, mid + 1, hi);
return root;
}
TreeNode *sortedArrayToBST(vector<int>& nums) {
return build(nums, 0, nums.size() - 1);
}
};
230-二叉搜索树中第 K 小的元素
执行中序遍历得到有序数组,取 res[k-1] 即可。时间复杂度为 O(N)。
class Solution {
public:
void dfs(TreeNode *root, vector<int> &res) {
if (!root) return;
dfs(root->left, res);
res.push_back(root->val);
dfs(root->right, res);
}
int kthSmallest(TreeNode* root, int k) {
vector<int> res;
dfs(root, res);
return res[k-1];
}
};
借用栈和迭代法,可以不必遍历整个二叉树得到完整数组,而是在找到第 K 个元素时就停止。也是一个中序遍历。
时间复杂度可以降到 O(H+K),其中 H 是树的高度。在栈开始 pop 之前,需要 H 次运算来到达叶子结点。
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode *> stk;
while (true) {
while (root) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
k -= 1;
if (k == 0) {
return root->val;
}
root = root->right;
}
return 0;
}
};
96-不同的二叉搜索树
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?
定义 f(n) = n 个节点组成的二叉搜索树的个数。
定义 g(i) = 以 i 为根节点的二叉搜索树的个数,对于 g(i),其左子树的节点数为 i-1,右子树的节点数为 n-i,因此 g(i) = f(i-1) * f(n-i)。
f(n) = g(1) + g(2) + ... + g(n) (1...n 每个数都可以作为根节点)。
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
};
目标和、排列组合问题
112-目标和(DFS)
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。叶子结点是没有子树的节点。
当前节点是否满足条件,左子树是否满足条件、右子树是否满足条件;这是一个深度优先搜索,且是前序遍历。
class Solution {
public:
bool hasPathSum(TreeNode* root, int target) {
if (!root) return false;
target -= root->val;
if (target == 0 && !root->left && !root->right)
return true;
return hasPathSum(root->left, target) || hasPathSum(root->right, target);
}
};
113-目标和 II(回溯法)
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
问完成一件事情的所有解决方案,一般采用回溯算法(深度优先遍历)完成。
解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
- 路径:存储已经访问的节点。回溯时,要将节点弹出。
- 结束条件:到达决策树叶子结点。
- 子树:当前可以走的路径,不断接近叶子结点。
class Solution {
public:
void dfs(TreeNode *root, int target, vector<int> &path, vector<vector<int>> &res) {
if (!root) return;
path.push_back(root->val); // 节点进入
target -= root->val;
if (target == 0 && !root->left && !root->right) {
res.push_back(vector<int>(path));
path.pop_back();
return;
}
dfs(root->left, target, path, res);
dfs(root->right, target, path, res);
path.pop_back(); // 节点弹出
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<vector<int>> res;
vector<int> path;
dfs(root, targetSum, path, res);
return res;
}
};
437-目标和 III(前缀和)
给定一个二叉树和一个目标和,找到总和等于给定目标和的路径总数。路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的。
简单的方法,延续上一题的思路,以每个节点为根节点,都算一遍和为 sum 的路径数。二叉树的 dfs 时间复杂度是 O(N),对 N 个节点的二叉树每个节点都执行一遍 dfs,运算次数等于 N * 树的高度,对于平衡二叉树时间复杂度是 O(Nlog(N)),极端情况下的斜二叉树时间复杂度为 O(N^2)。
求所有具体路径的,用回溯法;不求具体路径,仅求解的个数的,可以用前缀和、动态规划。
前缀和�:给定数组 nums,定义 prefixSum(n) = nums[0] + nums[1] + ... + nums[n] 为数组的前缀和。那么则有:
nums[n] = prefixSum(n) - prefixSum(n-1)
nums[i] + ... + nums[j] = prefixSum(j) - prefixSum(i-1)
相同的前缀和可能出现多次,如果 prefixSum(i) == prefixSum(j),那么 (i, j] 的区间的数的和一定为 0。
如果 prefixSum(i) + target == prefixSum(j),那么(i, j] 的区间的数的和一定为 target。
本题的关键技巧,是用哈希表记录 {key: 前缀和;value: 出现次数}。
class Solution {
public:
void dfs(TreeNode *root, int target, int prefixSum, unordered_map<int, int> &um) {
if (!root) return;
prefixSum += root->val;
res += um[prefixSum - target];
um[prefixSum] += 1;
dfs(root->left, target, prefixSum, um);
dfs(root->right, target, prefixSum, um);
um[prefixSum] -= 1;
}
int pathSum(TreeNode* root, int sum) {
unordered_map<int, int> um;
um[0] = 1;
dfs(root, sum, 0, um);
return res;
}
private:
int res;
};
560-目标和子数组(前缀和)
前缀和对于连续子数组求和问题特别有用!用哈希表记录 {key: 前缀和;value: 出现次数}。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int prefixSum = 0;
int res = 0;
unordered_map<int, int> um;
um[0] = 1;
for (int i = 0; i < nums.size(); ++i) {
prefixSum += nums[i];
res += um[prefixSum - k];
um[prefixSum] += 1;
}
return res;
}
};
39-组合的和(回溯法)
给定一个数组和一个目标数,找出所有可以使数字和为 target 的组合。数组中不存在重复数字,每个数字可以重复使用,解不能包括相同组合(同一组数字的不同排列是相同组合)。
对于这类寻找所有可行解的题,我们都可以尝试用「搜索回溯」的方法来解决。
class Solution {
public:
void dfs(vector<int> &nums, int target, vector<int> &path, vector<vector<int>> &res, int start) {
if (target < 0) return;
if (target == 0) {
res.push_back(vector<int>(path));
return;
}
for (int i = start; i < nums.size(); ++i) {
path.push_back(nums[i]);
dfs(nums, target - nums[i], path, res, i);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> res;
vector<int> path;
dfs(candidates, target, path, res, 0);
return res;
}
};
时间复杂度的分析,没有找到比较权威的评论,但大致是每个数字需要考虑选择和不选两种状态,因此上限是 O(2^N)。
40-组合的和 II(回溯法)
给定一个数组和一个目标数,找出所有可以使数字和为 target 的组合。数组中可能存在重复数字,每个数字只能使用一次,解不能包括相同组合。
例子:[10,1,2,7,6,1,5],target = 8;输出:[[1,1,6],[1,2,5],[1,7],[2,6]]。
因去重需要,进行排序。
class Solution {
public:
void dfs(vector<int> &nums, int target, vector<int> &path, vector<vector<int>> &res, int start) {
if (target < 0) return;
if (target == 0) {
res.push_back(vector<int>(path));
return;
}
for (int i = start; i < nums.size(); ++i) {
if (i > start && nums[i] == nums[i-1]) continue;
path.push_back(nums[i]);
dfs(nums, target - nums[i], path, res, i + 1); // nums[i] 已经使用了,从 nums[i+1] 继续搜索
path.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
vector<vector<int>> res;
vector<int> path;
dfs(candidates, target, path, res, 0);
return res;
}
};
216-组合的和 III(回溯法)
给定一个数组 [1, 2, 3, 4, 5, 6, 7, 8, 9] 和一个目标数,要求使用 k 个数,找出所有可以使数字和为 target 的组合。每个数字只能使用一次,解不能包括相同组合。
class Solution {
public:
void dfs(vector<int> &nums, int target, vector<int> &path, vector<vector<int>> &res, int start, int k) {
if (target < 0) return;
if (target == 0) {
if (path.size() == k) {
res.push_back(vector<int>(path));
}
return;
}
if (path.size() >= k) return;
for (int i = start; i < nums.size(); ++i) {
path.push_back(nums[i]);
dfs(nums, target - nums[i], path, res, i + 1, k);
path.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
vector<int> nums{1, 2, 3, 4, 5, 6, 7, 8, 9};
vector<vector<int>> res;
vector<int> path;
dfs(nums, n, path, res, 0, k);
return res;
}
};
70-爬楼梯(动态规划)
你需要爬 n 阶才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
只问方法个数,不问具体的路径,就可以不用回溯法。
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
};
377-组合的和 IV(动态规划)
给定一个数组和一个目标数,问有多少种方法组成目标数(数字和为目标数的组合的个数,不同的排列视为不同的组合)。数组中不存在重复数字,每个数字可以重复使用。
这道题是爬楼梯的升级版,即需要爬 target 阶,每一次可以爬 num in nums 阶,问有多少种爬法。直接延续上一题的解题思路即可。
C++ 计算 dp[i] 时数值可能已经溢出 int 范围,由于题目的返回类型是 int,肯定不可能输出是一个溢出 int 的数,因此该溢出项可以直接跳过。
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int> dp(target + 1);
dp[0] = 1;
for (int i = 1; i <= target; ++i) {
for (int num : nums) {
if (i >= num && dp[i] <= INT_MAX - dp[i-num]) {
dp[i] += dp[i-num];
}
}
}
return dp[target];
}
};
46-全排列(回溯法)
给定一个没有重复数字的数组,返回其全排列。
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
class Solution {
public:
void dfs(vector<int> &nums, int target, vector<int> &path, vector<vector<int>> &res, vector<bool> &visited) {
if (target == 0) {
res.push_back(vector<int>(path));
return;
}
for (int i = 0; i < nums.size(); ++i) {
if (!visited[i]) {
path.push_back(nums[i]);
visited[i] = true;
dfs(nums, target - 1, path, res, visited);
visited[i] = false;
path.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
vector<int> path;
int N = nums.size();
vector<bool> visited(N, false);
dfs(nums, N, path, res, visited);
return res;
}
};