排序、查找
912-数组排序(快速排序算法)
归并排序:原始数组 [4, 1, 3, 2];先排序左半边、再排序右半边,得到 [1, 4, 2, 3];最后合并成 [1, 2, 3, 4]。
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
N = len(nums)
aux = [0] * N # auxiliary 辅助数组,归并排序需要额外 N 的存储空间
self.sort(nums, aux, 0, N-1)
return nums
def sort(self, nums, aux, lo, hi):
if lo >= hi: return
mid = lo + (hi-lo)//2
self.sort(nums, aux, lo, mid)
self.sort(nums, aux, mid+1, hi)
self.merge(nums, aux, lo, mid, hi)
def merge(self, nums, aux, lo, mid, hi):
# copy to aux
for i in range(lo, hi+1):
aux[i] = nums[i]
# merge back to nums
i = lo
j = mid + 1
for k in range(lo, hi+1):
if i > mid: # 左半边的数取完了,取右半边的
nums[k] = aux[j]
j += 1
elif j > hi: # 右半边的数取完了,取左半边的
nums[k] = aux[i]
i += 1
elif aux[i] <= aux[j]:
nums[k] = aux[i]
i += 1
else:
nums[k] = aux[j]
j += 1
快速排序:
class Solution {
public:
int partition(vector<int>& nums, int lo, int hi) {
int i = lo + 1;
int j = hi;
while (true) {
while (i <= j && nums[i] <= nums[lo]) ++i;
while (i <= j && nums[j] >= nums[lo]) --j;
if (i >= j) break;
swap(nums[i], nums[j]);
}
swap(nums[lo], nums[j]);
return j;
}
void sort(vector<int>& nums, int lo, int hi) {
if (lo >= hi) return;
int pa = partition(nums, lo, hi);
sort(nums, lo, pa - 1);
sort(nums, pa + 1, hi);
}
vector<int> sortArray(vector<int>& nums) {
sort(nums, 0, nums.size() - 1);
return nums;
}
};
快速排序算法在平均状况下有着不错的表现�,但是对于基准值的选择十分敏感,最坏情况下的算法复杂度是 O(n^2)。C++ std sort 的实现选择了首部、中部、尾部三个元素的中值作为 pivot。
现实中应用的排序,往往根据数据集的特征,采用多种排序算法的混合。比如 C++ std sort 的实现被称为 Introspective Sorting(内省式排序),使用快速排序算法、分段排序;当分段的元素个数小于 16 时,采用插入排序,插入排序对“大部分有序”的数据集效率非常好;当递归层次过深、分割行为有恶化倾向时,采用堆排序,堆排序最坏时间复杂度也能保证 O(NlogN)。参考 std::sort 源码剖析。
215-第 k 大的数
找到数组中第 k 大的数,最容易想到的,用 O(NlogN) 排序,再用 O(1) 取第 k-1 个元素。
方案一:快速选择算法
与快速排序一样,都是由计算机科学家托尼·霍尔发明的。
快速排序中,有一个子过程称为分区,可以在线性时间里将一个列表分为两部分,分别是小于基准和大于等于基准的元素。
与快速排序一样,快速选择算法对于基准值的选择非常敏感,可以在切分函数的一开始,随机交换第一个元素与它后面的任意一个元素的位置。
它的时�间代价的期望是 O(n),证明过程可以参考「《算法导论》9.2:期望为线性的选择算法」。
class Solution {
public:
int partition(vector<int>& nums, int lo, int hi) {
int i = lo + 1;
int j = hi;
while (true) {
while (i <= j && nums[i] <= nums[lo]) ++i;
while (i <= j && nums[j] >= nums[lo]) --j;
if (i >= j) break;
swap(nums[i], nums[j]);
}
swap(nums[lo], nums[j]);
return j;
}
int findKthLargest(vector<int>& nums, int k) {
int N = nums.size();
k = N - k; // to find kth largest, means nums[N-k]
int lo = 0;
int hi = N - 1;
while (lo <= hi) {
int pa = partition(nums, lo, hi);
if (pa == k) {
return nums[k];
} else if (pa < k) {
lo = pa + 1;
} else {
hi = pa - 1;
}
}
return nums[k];
}
};
方案二:优先队列
优先队列天然就是解决 TopK 这种问题的。
考虑从 10 亿个数中找到最大/最小的 100 个数。首先空间上,样本数据如果特别大(例如 10 亿这种级别),并不适合一次性将所有数据读到内存中进行处理;第二时间上,可以将数据集分拆,充分利用多核 CPU 并行处理,提高效率。
以找最大的 100 个数为例(找最大则构建最小堆,找最小则构建最大堆),将样本集分成 1,000,000,000 / 100 = 1,000,000 份,每份找到最大的 100 个数,最终整体的最大 100 个数必定在这中间产生。对每一份,用前 100 个数构建最小堆,再遍历剩余的数,如果小于堆顶则直接跳过;如果大于堆顶则将它放到堆里,同时调整堆。这样遍历完之后,这个最小堆就是这一份样本中最大的 100 个数。
- 当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。
- 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> topK;
for (int i : nums) {
if (topK.size() < k) {
topK.push(i);
} else if (i > topK.top()) {
topK.push(i);
topK.pop();
}
}
return topK.top();
}
};
347-Top K 高频元素
给定一个数组,返回其中出现频率前 k 高的元素。
优先队列天然就是解决 TopK 这种问题的。
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> um;
for (int i = 0; i < nums.size(); ++i) {
um[nums[i]] += 1;
}
auto cmp = [&um](int lhs, int rhs) { return um[lhs] > um[rhs]; };
priority_queue<int, vector<int>, decltype(cmp)> topK(cmp);
for (const auto &kv : um) {
if (topK.size() < k) {
topK.push(kv.first);
} else if (kv.second > um[topK.top()]) {
topK.pop();
topK.push(kv.first);
}
}
vector<int> res;
while (!topK.empty()) {
res.push_back(topK.top());
topK.pop();
}
return res;
}
};
973-最接近原点的 K 个点
class Solution {
public:
vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
auto cmp = [](const vector<int> &lhs, const vector<int> &rhs) {
return (pow(lhs[0], 2) + pow(lhs[1], 2)) < (pow(rhs[0], 2) + pow(rhs[1], 2));
};
priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)> topK(cmp);
for (vector<int> &point : points) {
if (topK.size() < k) {
topK.push(point);
} else if (cmp(point, topK.top())) {
topK.pop();
topK.push(point);
}
}
vector<vector<int>> res;
while (!topK.empty()) {
res.emplace_back(std::move(topK.top()));
topK.pop();
}
return res;
}
};
295-从数据流中找中位数
设计一个支持以下两种操作的数据结构:添加一个整数到容器中;返回容器中所有元素的中位数。
方案一:插入排序可以将一个数字插入到列表中并继续保持列表有序。二分查找的时间复杂度是 O(logN);插入时因为要移动插入位置后面的所有元素,因此时间复杂度是 O(N)。总时间复杂度是 O(N)。
class MedianFinder {
public:
void addNum(int num) {
if (vec.empty()) {
vec.push_back(num);
} else {
auto ite = lower_bound(vec.begin(), vec.end(), num); // 二分查找
vec.insert(ite, num); // 插入
}
}
double findMedian() {
int n = static_cast<int>(vec.size());
if (n % 2 == 0) {
return (vec[n/2-1] + vec[n/2]) * 0.5; // 注意整型相除结果 3 / 2 = 1,所以要用 * 0.5
} else {
return vec[n/2];
}
}
private:
vector<int> vec;
};
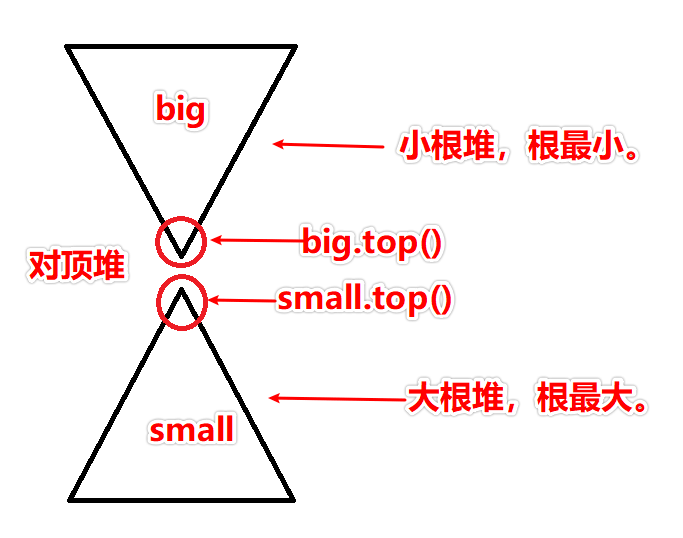
方案二:这题我们关心的仅仅是中位数,并不需要保持整个数组有序,因此方案一肯定是有优化空间的。我们使用两个堆,将所有比中位数小的数放在 small 堆(大根堆、根最大),比中位数大的数放在 big 堆(小根堆、根最小),并且保证两堆容量之差小于等于 1。那么,中位数就一定在两个堆的堆顶之中。
class MedianFinder {
public:
void addNum(int num) {
if (small.empty()) {
small.push(num);
++N;
return;
}
if (num <= small.top()) {
small.push(num);
} else {
big.push(num);
}
if (small.size() > 1 + big.size()) { // 注意 size_type 是无符号数,不要相减!!
big.push(small.top());
small.pop();
} else if (big.size() > 1 + small.size()) {
small.push(big.top());
big.pop();
}
++N;
}
double findMedian() {
if (N % 2 == 0) {
return (small.top() + big.top()) * 0.5;
} else {
return small.size() > big.size() ? small.top() : big.top();
}
}
private:
priority_queue<int> small;
priority_queue<int, vector<int>, greater<int>> big;
int N = 0;
};
方案三:能够同时满足高效插入、搜索的数据结构是什么?——红黑树。红黑树可以以 O(logN) 时间插入元素并保持自平衡;而中位数就是根节点、或根节点与它的一个子树的均值。
红黑树在 C++ 的实现是 set,由于本题可能出现相同数字,因此我们需要用 multiset,并维护一个指针:当数组大小为奇数时,指向中位数;当数组大小为偶数时,指向中间两个数值中较大的那个。
class MedianFinder {
public:
void addNum(int num) {
const size_t N = data.size();
data.insert(num);
if (N == 0) {
mid = data.begin();
} else if (num < *mid) {
mid = N & 1 ? mid : prev(mid);
} else {
mid = N & 1 ? next(mid) : mid;
}
}
double findMedian() {
const size_t N = data.size();
if (N & 1) {
return *mid;
} else {
return (*prev(mid) + *mid) * 0.5;
}
}
private:
multiset<int> data;
multiset<int>::iterator mid;
};
27-移除数组中指定元�素(同向双指针)
给定一个数组,在原地删除数值等于 val 的元素,返回移除后数组的新长度。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i = 0; // [0, i] 区间是符合条件的结果
for (int j = 0; j < nums.size(); ++j) {
if (nums[j] != val) {
nums[i] = nums[j];
++i;
}
}
return i;
}
};
26-删除排序数组中的重复项(同向双指针)
给定一个非递减数组,在原地删除重复的元素,使得每个元素只出现一次,返回移除后数组的新长度。
这个思路可以总结为“同向双指针”,即两个指针朝同一个方向移动,一快一慢。快指针用于遍历,慢指针在每个循环体中,始终保持满足题目条件。
此题中,慢指针 i 始终指向结果数组的右边界,始终保持 nums[0, i] 是符合题目条件的数组。
由于数组有序,i 始终指向最后找到的非重复元素,当 j 遍历到一个与 i 不相同的值,就代表找到了一个新值,此时移动慢指针到下一个位置,并覆盖。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.empty())
return 0;
int i = 1;
for (int j = 1; j < nums.size(); ++j) {
if (nums[j] != nums[j-1]) {
nums[i] = nums[j];
++i;
}
}
return i;
}
};
80-删除排序数组中的重复项 II(同向双指针)
给定一个非递减数组,在原地删除重复的元素,使得每个元素最多出现两次,返回移除后数组的新长度。
与上题思路一样,注意初始时慢指针的边界,以及移动慢指针的条件即可。拓展到每个元素最多出现 k 次,也是一样的做法。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.size() <= 2)
return static_cast<int>(nums.size());
int i = 2;
for (int j = 2; j < nums.size(); ++j) {
if (nums[i-2] != nums[j]) {
nums[i] = nums[j];
++i;
}
}
return i;
}
};
283-移动零(同向双指针)
给定一个数组,将所有 0 移动到数组的末尾。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int i = 0;
for (int j = 0; j < nums.size(); ++j) {
if (nums[j] != 0) {
nums[i] = nums[j];
++i;
}
}
for (int j = i; j < nums.size(); ++j) {
nums[j] = 0;
}
}
};
75-颜色排序
这是计算机科学经典的荷兰国旗问题。1, 2, 3 代表红白蓝三色,给定数组 [2,0,2,1,1,0],排序成 [0,0,1,1,2,2]。
要把数组分成三个颜色,我们可以用双指针 left, right 框定好 “1” 的范围,最终的结果是,nums[left...right] 都是 1、left 的左边都是 0、right 的右边都是 2。
class Solution {
public:
void sortColors(vector<int>& nums) {
int lo = 0;
int hi = static_cast<int>(nums.size()) - 1;
int i = 0;
while (i <= hi) {
if (nums[i] == 0) {
std::swap(nums[lo], nums[i]);
++lo;
++i;
} else if (nums[i] == 1) {
++i;
} else {
std::swap(nums[i], nums[hi]);
--hi;
}
}
}
};
如果扩展到四色呢?有一种遍历两次的方法,第一次遍历先记录每个颜色的个数,第二次遍历将每个颜色放到对应位置即可。
class Solution {
public:
void sortColors(vector<int>& nums) {
unordered_map<int, int> um;
for (int i : nums) {
++um[i];
}
for (int i = 0; i < nums.size(); ++i) {
if (um[0] > 0) {
nums[i] = 0;
--um[0];
} else if (um[1] > 0) {
nums[i] = 1;
--um[1];
} else {
nums[i] = 2;
--um[2];
}
}
}
};
977-有序数组的平方
给定非递减数组 A,返回每个数字的平方组成的新数组,要求也按非递减排序。
遇到的阿里面试真题。如果直接乘方然后排序,计算次数是 N + NLogN,复杂度是 O(NLogN)。本题中可以利用有序数组、求平方这两个特性,做一些技巧,降低计算次数。
方案一:找到第一个大于零的数,用两个指针分别向左右遍历。
方案二:利用原数组的特性:两边的平方大,中间的平方小。
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int N = nums.size();
vector<int> res(N, 0);
int lo = 0;
int hi = N - 1;
for (int i = N - 1; i >= 0; --i) {
if (abs(nums[lo]) > abs(nums[hi])) {
res[i] = pow(nums[lo], 2);
++lo;
} else {
res[i] = pow(nums[hi], 2);
--hi;
}
}
return res;
}
};
34-在排序数组中查找元素的第一个和最后一个位置
给定一个非递减数组,找出目标值在数组中的开始位置和结束位置。
输入:nums = [5,7,7,8,8,10], target = 8;输出:[3,4]。
二分法+线性查找:
class Solution:
def binarySearch(self, nums, target, lo, hi):
if lo > hi: return -1
mid = (lo + hi) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
return self.binarySearch(nums, target, lo, hi-1)
else:
return self.binarySearch(nums, target, lo+1, hi)
def searchRange(self, nums: List[int], target: int) -> List[int]:
index = self.binarySearch(nums, target, 0, len(nums)-1)
i = index - 1
j = index + 1
while i >= 0 and nums[i] == target:
i -= 1
while j < len(nums) and nums[j] == target:
j += 1
return [i+1, j-1]
69-平方根
方案一,一个数的平方根不会超过它除以二,因此我们可以在 [2, x/2] 范围内进行二分查找。
class Solution {
public:
int mySqrt(int x) {
if (x <= 1) return x;
long hi = x / 2;
long lo = 0;
while (lo <= hi) {
long mid = lo + (hi - lo) / 2;
long y = mid * mid; // mid * mid 可能会超出 int 的范围
if (y > x) {
hi = mid - 1;
} else if (y < x) {
lo = mid + 1;
} else {
return static_cast<int>(mid);
}
}
return static_cast<int>(hi);
}
};
方案二,牛顿迭代法。